Note on generalizations: this blog post covers a large span of topics. Some MEV experts may object to some of the simplifications I made to make this story more understandable. Some casual readers may find this too complex to follow. I tried to find a happy medium but probably didn’t succeed. Let me know if you have any concrete suggestions for improvement.

The email invitation

Just months away from the final exam that would grant me my master’s in Computer Science and my evenings and weekends back, the email arrived. The title: “Application of Bellman-Ford to new crypto markets”.

Interesting. While starting a new project was the last thing on my mind after spending the previous two years grinding away on OMSCS homework and the year prior building a series of intellectually but not particularly financially successful trading bots on centralized crypto exchanges, I couldn’t help but respond. The crypto market had been dead for a couple years, but I started to detect signs of life and wasn’t sure what else I would do with my post-graduation freedom while the world was still locked down.

A quick call delivered me more details. In 2017-2018, the general paradigm for crypto was to either buy-and-hold in one’s own wallet or swap via centralized exchanges. There wasn’t all that much you could do with cryptocurrencies on-chain (with some exceptions–RIP EtherDelta).

Since then, a new innovation had taken hold: the smart contract. Smart contracts deployed on Ethereum and other blockchains enabled two (or more) users to swap tokens, lend money, or engage in other types of transactions without a central intermediary. This created a huge opportunity for an aspiring arbitrageur. Can you see why?

By mid-2020, the centralized exchanges (CEXes) had become very efficient. Volume had consolidated (onto Binance, FTX, Coinbase, Kraken, and so on), professional market makers dominated (Alameda, Wintermute, SCP, Jane St., etc.), and the universe of tradable instruments remained relatively small as each new ticker had to be approved by the CEX leadership and backed with some guarantee of reasonable liquidity from market makers.

Decentralized exchanges (DEXes) did not have any of these attributes. Trading volume was fragmented across dozens of venues, each jockeying for position with various tricks like SushiSwap’s vampire attack. The cost of trading was generally very high (hundreds rather than tens of basis points on CEXes) because sophisticated market makers were only beginning to enter the system, liquidity was scarce, and they relied on capital-inefficient mechanics to function. And most importantly, no gatekeeper existed to control listing or ensure liquidity. Any user could create a COIN_1/COIN_2 instrument on any DEX that would create another potentially profitable arbitrage opportunity. With the advent of DEXes, the trading universe expanded by approximately two orders of magnitude.

Together with the fact that significant volume was moving from CEXes to DEXes, these changes meant that times were getting good again for amateur arbitrageurs. Two days later, another email arrived in my inbox with the subject, “Invitation to join DeFi trading project”.

Brief detour on how DEXes/{CF,A}MMs work

Note: skip this section if you are already familiar with how {CF,A}MMs work, which is a prerequisite to the rest of the blog post.

Centralized exchanges like Binance, Coinbase, NYSE, and NASDAQ match buyers and sellers with a central limit order book (CLOB). Patient buyers and sellers post limit orders representing the price and size that they are willing to buy or sell a given asset. Impatient buyers and sellers place market orders that burn through the CLOB until the desired size is reached.

This approach works really well for when the universe of tradable instruments is relatively small and some actor, a market maker, is willing to take the risk of placing limit orders (and correspondingly holding positions in both assets being traded) in exchange for collecting the premium between the best bid and the best ask. Without this actor or large uncorrelated trading volumes, price discovery fails, spreads widen, and trading ceases. We observe this to some extent in the housing market today where rising rates have driven the bid/ask spread to a level that is unacceptable to both sellers and buyers, dropping volume to a fraction of its typical level.

This problem can be solved with automatic or constant-function market maker (AMM). Instead of requiring an agent to dynamically provide and withdraw liquidity on a CLOB, an AMM does the same thing passively with an equation and bucket of capital.

Different AMMs use different functions, but the most common approach is constant product. This function, popularized by Uniswap V2, requires that the value of two assets in the AMM contract, called a pool from now on, remain equal. To translate English to math, (R_α −∆_α)(R_β +γ∆_β) = k, where ∆_α is the amount withdrawn from the pool, ∆_β is the amount deposited into the pool, R are the corresponding reserves (buckets of capital), and γ is the trading fee. These conditions are analyzed in much more detail in Guillermo Angeris’s canonical paper, An Analysis of Uniswap Markets.

Functionally, what this means is that anyone can create a market by depositing equal (in value) amounts of two coins without asking an exchange for permission or incentivizing a sophisticated third party to make the market. These depositors, called liquidity providers or LPs, are rewarded for their service in two ways: by creating a new market for a project or coin that they believe in and by fees that are generated from each swap. Each one of these markets is referred to as a pool.

Brief detour on liquidations

Note: skip this section if you are already familiar with how DeFi liquidations work. This is not a prerequisite to understanding the rest of this blog post, but I do mention liquidations several times in the text.

In addition to enabling users to swap assets without a central intermediary, smart contracts facilitate lending. The mechanics are much simpler than swaps. Alice and Bob both deposit funds into a lending contract (Aave, Compound, Maker, etc.). As long as Bob leaves his original funds locked in the protocol, he can withdraw ~50% more (this number depends on the protocol and asset) at some algorithmically determined rate that gets paid to Alice for providing the funds. This lets Bob create a short position, reinvest for a levered long, or withdraw spending money without selling the underlying and incurring a taxable event and Alice to generate a return on her capital.

The whole system works without any centralized system of enforcement because a liquidation reward is paid out to any address that flags loans that have crossed their collateralization threshold. This reward motivates traders to build systems that monitor the mempool and the external oracles that provide price information to the blockchain to compete to liquidate loans the moment they go bad. For those who would like to learn more, Anton Evangelatov discusses building such a bot on his blog.

Brief detour on arbitrage (atomic, statistical, and otherwise)

Note: skip this section if you are already familiar with how arbitrage works on blockchains. This may be worth reading if you are only familiar with arbitrage in traditional financial markets.

In traditional capital markets, arbitrage typically refers to buying something on one venue and selling it on another (possibly through a series of intermediate transactions) for a higher price. However, in the most technical sense, these transactions are not truly risk-free. Prices can move mid-transaction, intermediate hops can fail to fill, counterparties can default, and so on. I observed this clearly while running my CEX arbitrage strategy. Often, I would detect a profitable trade, e.g. BTC → ETH → USDT → BTC, but find myself left with less BTC than I started with because the price on one of the legs moved against me before I could complete the transaction.

When trading on DEXes, arbitrage (often called atomic arbitrage to differentiate from the strongly statistical arbitrage described above) is truly risk-free (excluding hacks and other types of attacks that we will discuss later). A smart contract can be written to either execute every leg of the trade and confirm profitability or revert, even across trading venues (DEXes).

Even better, the pools themselves can serve as a source of capital. If the trade size in the example above was 1 BTC, one could borrow the funds from the BTC/USDT pool, swap that BTC for ETH in the BTC/ETH pool, swap the ETH for USDT in the ETH/USDT pool, and return the USDT to the USDT/BTC pool to close the loop and pocket the USDT left over. Atomic arbitrage is probably the most capital efficient and least risky trading strategy ever created.

While this blog post largely covers atomic arb, non-atomic (cross-chain, CEX/DEX, etc.) arb opportunities also exist in crypto and are likely an order of magnitude more profitable and less accessible due capital requirements and risk profile.

Brief detour on the optimal data structure for representing DEXes and CFMMs

Note: skip this section if you are already familiar with the most common way of representing trading pairs with a graph.

With dozens of DEXes and thousands of potential trading pairs, one needs to think carefully about how to represent the state of the system. Fortunately, foreign exchange traders have already developed a fairly optimal solution to the problem. They create a graph of all possible trading opportunities with the nodes representing coins and the edges representing rates. If more than one rate exists, e.g. two DEXes offer the same instrument at inevitably two slightly different prices, more than one edge is drawn between two nodes, creating a multigraph.

To find an arbitrage opportunity on such a data structure, one needs to find a closed loop of edges for which the product of the weights is greater than one. A number of relatively efficient algorithms have been devised to do this, e.g. Bellman-Ford, Ford-Fulkerson. Throughout this post, I will interchangeably refer to coins as nodes, prices/pools as nodes, potential arbs as cycles, and profitable arbs as negative cycles, reflecting this graph representation. 

Note that this is by no means the only way to represent these DEXes. Angeris et al. show that representing the system as a bipartite graph with CFMMs and tokens as nodes and edges designating which tokens are traded on which venue makes calculating the optimal arbitrage path easier. While I never experimented with this approach, I believe it could solve some of the problems I discuss later in the post.

Back to our story: Arb on Ethereum was (and is) competitive

My new partners had already laid a strong foundation for our decentralized arb bot. Anton had previously written a successful liquidation bot and Nathan some software to analyze the entire network of pools. We needed to adapt the previous liquidation work to the new task. 

This involved several subsystems:

1. An opportunity-finder that would scan the blockchain to find all listed instruments and prune that set into a manageable graph using some heuristics like volume, recency, and risk.
2. A listener to pass the state of the Ethereum blockchain to our bot including the reserves in each pool, the current gas prices, the state of our workers, and (later) the transactions in the mempool.
3. A graph-maintainer that would consolidate all reserve changes into an up-to-date snapshot of the market.
4. An arb-finder that would generate a profitable trade from a graph.
5. An order executor that would package and sign the trade and send it to a miner.
6. An arb contract that would execute our instructions on-chain and revert if the trade were not profitable.

To put this in plain language, the basic idea then was that the bot would generate the graph offline on boot (this is slow), update the edge weights with every new block, and analyze the graph for profitable trades. If one existed, the bot would estimate the gas bid needed to land in position zero (ahead of competitors) in the following block and send a transaction containing size, path, and gas price to the miners. If the transaction were successful, the profit minus the gas costs would be deposited to our contract. If not, the transaction would revert, but we would be stuck with the gas bill.

The listener and graph maintainer could largely be reused from the liquidation bot, but we needed to write an algorithm to calculate path and write a contract to execute this new time of order. While the former was solved by vanilla Bellman-Ford for my previous CEX bot, it wouldn’t do for the DEX bot for a few reasons:

1. Bellman-Ford returns the percentage rather than absolute profit of a negative cycle, which makes it difficult to include an absolute gas cost in the graph (fees on DEXes are composed of relative trading fees, e.g. 0.3%, and absolute gas costs, e.g. 0.03 ETH). 
2. Bellman-Ford terminates after finding its first negative cycle. This means that in a block there might be both a $10k arb and a $0.10 one and the algorithm would have a 50/50 chance of returning either.
3. Bellman-Ford is deterministic. In the example above, the solution isn’t simply to re-run BF twice to find both.

On a CEX with relatively few assets, deep liquidity, many competitors, continuous price information, and no gas fees, none of these issues are a problem. If a negative cycle is detected, it is by-definition profitable and likely the only trade available.

On a DEX, this is almost never the case. A very large graph (we pruned ours to ~1k nodes) that batched hundreds of transactions into a single block of price updates will inevitably contain many, many negative cycles. And because on-chain transactions require gas payments that are variable and independent of order size, many of these negative cycles are not even profitable. Practically, this means that returning a single negative cycle for a given block will almost never yield a trade worth making.

To solve this problem, we slightly modified Bellman-Ford. After detecting a negative cycle we would delete a random edge in that cycle and then rerun the algorithm. This could be repeated N times to generate N negative cycles that were all potentially profitable. While this approach doesn’t guarantee any kind of optimality it runs relatively quickly (N* O(edges*nodes)) and is easy to implement.

Determining profitability was also a little bit of a challenge. Sizing an arb order on a CEX is very simple: calculate the largest order possible using the best bid or ask from each leg. The chances of an arb emerging two levels deep in the order book is very small. On a DEX, there is usually no notion of order book. Pricing is continuous along a curve determined by that venue’s function.

To determine whether a negative cycle would be profitable, we needed to use this curve to determine the optimal size, run that size through the arb path, and subtract estimated gas fee (the exchange fees were already included in the edge weights). Practically, this meant that we used binary search to determine optimal size for each negative cycle, which usually converged in ~10 steps, meaning that we needed to compute ~100 fairly complex calculations in each block, which was taking hundreds of milliseconds even running in parallel on a beefy machine.

With these algorithms written, we were ready to start trading. We loaded up our contact with a few ETH (we always started and ended with ETH to avoid having to hold multiple currencies) and set the bot loose on mainnet. After a few trades, we immediately identified two problems:

1. Other bots were not only reading the state of block N when sending trades to block N+1 but also monitoring the pending transactions in the N+1 mempool (the mempool is where proposed transactions are circulated before being confirmed on a block). While this would later manifest itself in a strategy called backrunning that we will discuss later, here the issue was with gas price. We predicted the gap price using information we had from block N but competitors would read our gas price from our transaction in the mempool and usually outbid us by 1 gwei.
2. This business was really high risk. The game theory optimal gas price to pay for a given arb is essentially the value of that arb. To put this concretely, if a $10k arb exists and two bots are bidding up the gas price to get their transactions confirmed, they are both incentivized to bid gas right up to that value (and actually beyond; paying $10.1k to win a $10k transaction results in a net loss of $100 while paying $9.9k to lose a $10k transaction results in a net loss of $9.9k). Practically, this didn’t happen because the time for these bidding wars was constrained by the block time, but losing multiple transactions in a row with high gas prices could absolutely wipe out a poorly capitalized trader. This would later be resolved with Flashbots, but at that point, only a handful of miners were experimenting with this approach to block building.

Solving #1 was relatively easy. We wrote a mempool listener to track the highest gas bid in block N+1, modified our order-calculating module to enable recalculation of profits with higher gas prices, and adapted our order executor to resubmit orders with a higher gas price.

However, #2 was tricky and perhaps intractable. Over the course of the O(weeks) it took us to get our system up and running, competition in the mempool heated up. It was clear that the key to winning on Ethereum was some combination of finding arbs that others missed, understanding network dynamics involved in getting transactions to miners ahead of the competition, and having very high tolerance for risk and drawdowns. However, this would all become moot as a new opportunity emerged.

Enter Avalanche

As we were struggling to ramp up on Ethereum mainnet, a trend was emerging. Alternative L1s like Matic (now Polygon), Avalanche, NEAR, BSC, Fantom, and Solana were beginning to attract attention. A large subset of them retained significant parts of the Ethereum Virtual Machine but added some twist to the consensus mechanism to increase throughput. 

Avalanche was most interesting to us because it did away with the mempool altogether, eliminating our biggest problem. Instead, Avalanche adopted a leader-less block production model where any validator could produce a block at any time and gas price was fixed at 225 gwei (both of these features would later change). Rather than needing to monkey with winning expensive gas auctions, we could propose our own block whenever an arb appeared. Speed would anoint the winner and the risk of losing an auction would decrease from potentially tens of thousands of dollars to a few cents.

In addition, the first DEX on Avalanche, Pangolin, had just launched and began to attract some volume. It offered relatively few instruments, making it much easier to construct and process the graph and find profitable cycles. Given our lack of success on Ethereum (I think that we had made a few thousand dollars profit at this point but were largely outsiders), we spent a long morning editing RPC endpoints, spinning up an Avalanche node, and adapting our order executor to the Pangolin router before bothering to deploy our own smart contract (it is possible to send arb orders to the DEX routers, but the profit guarantee is lost).

A few anxious minutes after launching, we fired our first transaction. It succeeded! We were $0.81 richer before paying for gas because our computer program was listening to updates on a somewhat obscure blockchain and firing out transactions to profit from inefficiencies. And hilariously, this $0.81 had been lying on the sidewalk for 3 blocks and about 30 seconds. There was literally no one keeping prices efficient on Avalanche.

A quick recap of how this works. Alice swaps PNG for USDT. Because there is limited capital in the USDT/PNG pool, the price moves against her by let’s say 5%. The price for PNG in terms of USDT is now 5% lower than equilibrium. An arbitrageur needs to find a path that lets her reverse that trade, e.g. swap USDT for PNG, to restore equilibrium. In the case of our first trade above, we were able to put together a cycle from WAVAX to USDT to PNG to UNI and back to WAVAX that was able to claim back some fraction of the 5% slippage minus the gas, slippage, and trading fees.

Shockingly, our bot kept spitting out trades. $1 profit one minute. $5 the next. Pretty soon all of these little arbs were adding up to real money. We had built a money machine.

How an end to our fun forced us to learn the Avalanche gossip protocol

For a few weeks, our little money machine hummed along without missing a beat. We built dashboards and monitors and established on-call rotations and dug in for the long haul. But then the printer stopped. Our transactions started landing behind competitors and reverting. The fun was over.

At that point, the universe of tradable instruments was still very small and only Pangolin and Zero (a newer DEX) had any kind of volume. There wasn’t much we could do to optimize the graph. On the code side, we made a few optimizations including delaying garbage collection, caching the contract ABI, and subscribing to logs rather than newHeads (these are both subscriptions supported by EVM-style nodes that deliver information about new transactions), which we found was a few milliseconds faster, but none of this made that much of a difference.

On a whim, we decided to connect our bot to a validator with around 10k AVAX staked instead of the regular node we were using for trading. Boom! The machine turned back on. We weren’t exactly sure what happened, but we were back in business.

The next few months were a battle for stake. Our bot would oscillate between 0% and 100% market share depending on what partner we managed to convince to share her validators. It was clear that the path to long-term victory on Avalanche was dependent almost entirely on stake at that point and business development rather than software development would dominate our mindshare.

It wasn’t immediately clear why stake was so important. The Snowman consensus protocol used by Avalanche’s C-Chain allowed any validator to propose a block. Why would a larger validator have an advantage?

It all came down to sampling. Snowman-vintage validators would gossip new blocks to one another through a number of different message types. When a new potentially arb-creating transaction was proposed, the validator or node through whom it was communicated via its RPC endpoint, sent a PushQuery message to default 10 peers. Those 10 peers gossiped to 10 more and so on until a tipping point of validators accepted the block. This is described in more detail in the Ava Labs whitepaper. The PushQuery message contains both the peer nodes’ preference for the tip of the blockchain and the proposed new block. The sooner one receives and decodes this message, the sooner one can update the graph and fire an arb out in response. Being one of those first 10 nodes was a huge competitive advantage.

Those 10 nodes were selected via a stake weighted process. The probability of hearing about a transaction first scaled linearly with the stake of that node. Thus, a bot connected to a massive AVAX stake would have a nearly insurmountable advantage in arbitrage on Avalanche without access to a large edge elsewhere.

6 months of tricks

The next six months were a battle on the blockchain. As interest in the Avalanche blockchain heated up, the competition for the growing arbitrage profits grew fiercer. Several very strong teams were backed by several groups with tens of millions of dollars in staked AVAX and market share swung wildly back and forth. Rather than getting bogged down in the details, I wanted to share a few fun examples of hacks that vaulted us back into the lead every time we thought we were down and out.

Remove timer in Avalanche Coreth

By default, the AvalancheGo node holds a block for between 2 and 3 seconds to accumulate transactions before gossiping to peers. While it seems extremely obvious that this timer would hurt a team trying to profit from speed, it was quite some time before arb teams started digging into the code to find and remove speed bumps like this. This little change 10x’ed our market share for a few weeks.

Spam peers with PullQuery messages

Getting a PushQuery message in the first round is best, but one needn’t wait around to receive a new transaction as the vanilla protocol ordains. The Ava Labs docs aren’t super clear, but a PullQuery message is sent to another node to learn of its current preference. Rather than wait for a PushQuery message to arrive with the content of block N+1, a node can send PullQuery messages every millisecond with the ContainerID of N to every node to check if any of them have learned of N+1, which they communicate via a Chit. Once a new ContainerID is received, the node immediately responds with a Get message, which receives a Put in response and contains the new transaction, which is then decoded and used to update the graph.

All of these messages are a bit slow to send and decode, but this technique enabled a regular node with no stake to achieve ~5% market share against competitors with millions of AVAX staked.

Prune cycles and replace Bellman-Ford

At this point, the number of tokens, pools, and DEXes began to explode on Avalanche. Manually whitelisting tokens and DEXes to create the graph was no longer scalable and the problems with Bellman-Ford mentioned earlier began to manifest themselves. Small arbs were blinding our algorithms to large potential profits. There was a pareto-esque distribution of arb profits and ensuring we tried for the big fish was far more important than a slight speed edge across all opportunities. We really did need to find the largest possible profit in every block.

However, no closed-form algorithm existed to find the most negative cycle, much less the most profitable cycle through a given graph (Guillermo’s paper referenced above should do this, but he had not yet published this work and I never took the time to verify the results). Instead, we had to check profits for every cycle by brute force.

Given that the number of cycles scales exponentially with graph size, we needed to prune this rapidly growing graph and prioritize the cycles we checked for opportunities. To prune the graph, we required heuristically determined minimum pool balances (~$5k), recent activity (>1 transaction in the last 14 days), and no fee-on-transfer tokens. To prune the cycles, limited ourselves to cycles length 4 or less and ranked them according to trailing 30-day profits. When a transaction came in that modified the balance of a pool contained in our graph, we checked the top 1024 cycles containing that pool for potential arbitrage.

These optimizations dropped our time to check for a potential arbitrage from hundreds of milliseconds to tens, but this was still too slow.

Analytically calculate order size

While checking each cycle increased our profits, it decreased our speed. Calculating the optimal order size by binary search for 1024 different cycles was costing us market share. Calculus would come to the rescue.

The vast majority (perhaps all at that point?) of trading on Avalanche was through UniswapV2 clones. This means that every DEX used the same constant-product function (images shamelessly stolen from another one of Guillermo’s papers).

If we solve for ∆_β, we generate Uniswap’s well-known getAmountOut function, γ∆_αR_β/(R_α+γ∆_α). Note that if we assume that the reserves are constant, which they are between transactions, this equation is differentiable with respect to ∆_α, amountIn. This means that we can recursively create getAmountOut functions for equations of any length, take the derivative, set it equal to zero, and calculate the optimal order size.

The only problem is that this math is REALLY messy with some clever simplifications. The equation below is the derivative of a three-legged Uniswap arb (x=amountIn).

Fortunately, this simplifies nicely for the types of people who can look at the expressions above and recognize that they are just a collection of sums and products.

This equation sped up order size calculation by another factor of ten, dropping us into the millisecond range from receiving a new transaction to firing an arb.

Optimistic recursive order execution

The combination of these optimizations and continued success on the partnerships front vaulted us into the lead in the Avalanche arb race. However, we still had one last problem left to solve: the best arb for a given graph doesn’t necessarily extract all the inefficiencies out of the graph. A large arbitrage transaction could itself create a new arbitrage opportunity. Or two or more transactions might be necessary to fully capture the arbitrage created by the target transaction.

Since we faced this problem, several clever algorithmic approaches have been proposed, but we took a pretty darn good shortcut. When sending an arb, we would assume that it succeeded, update our reserve values accordingly, check for another, and so on. We would recursively send transactions until all the arb was gone, ensuring that there wasn’t anything left for our competitors.

Victory at last (for a while)

All this hard work paid off. By July, we had reached a ~90% market share in Avalanche arbitrage and even casual observers started to notice.

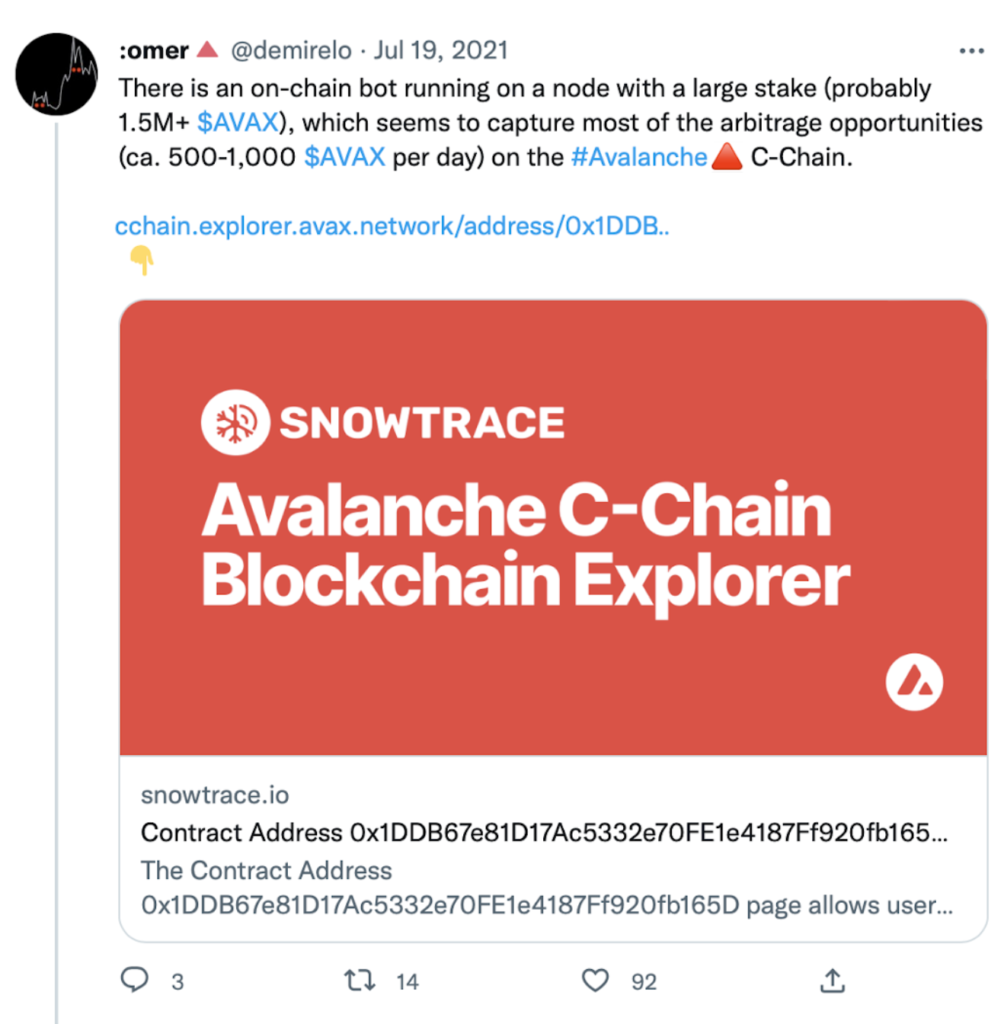
Congestion on the chain and the birth of Snowman++

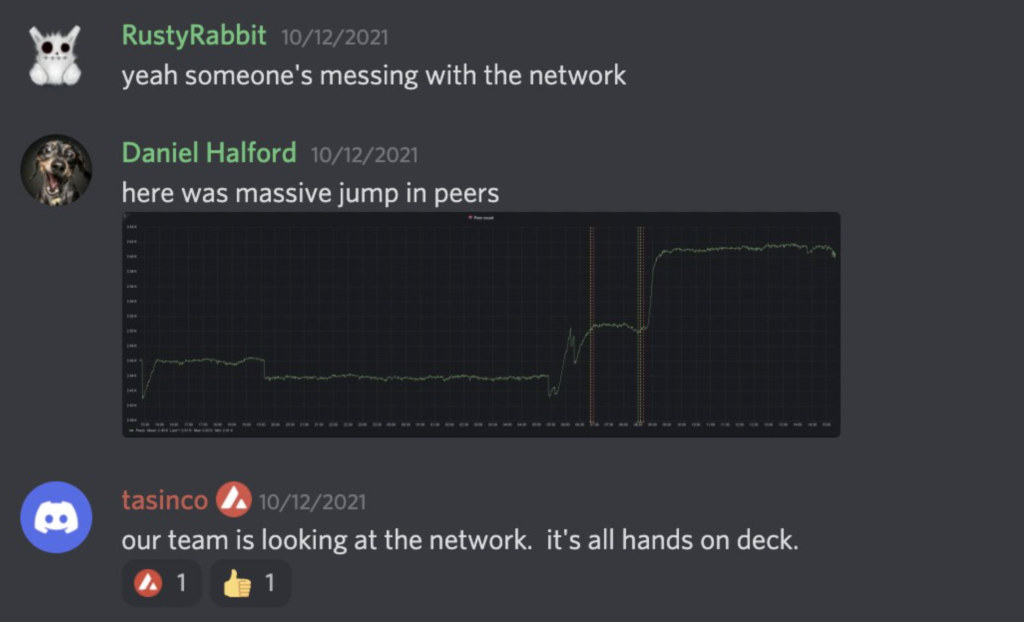
The good times did not continue to roll. As the battle for stake and speed played out, a very strong competitor emerged. Every block was contentious as our two teams raced for every transaction. The very foundation of the leaderless Avalanche protocol began to quake. Essentially every potential arb created a forked chain that required reconciliation between the validators. The Avalanche team responded with Snowman++.

This hard fork shifted the consensus engine toward what would become the Ethereum proof-of-stake model. Rather than allowing any validator to emit a block at any time, the next N validators were selected to produce blocks via a stake-weighted mechanism. The first validator on deck would have a window of M seconds to create a block or the opportunity would pass to the next one. If all N failed to propose a block, any validator could step in.

Snowman++ immediately had the desired effect. The moment it took effect, contention dropped to near zero and more transactions began appearing in each block. It also totally changed the game of arbitrage on Avalanche.

To succeed in a Snowball++ world, it was necessary to go back to some of the lessons we learned in Ethereum. Rather than mine transactions as soon as they were received (or with a small delay, depending on whether one adjusted the timers), transactions were held and batched into blocks at regular intervals. This means that a transaction would have already been broadly shared for many seconds before appearing on-chain. If one waited until the transaction was included in a block, she would find that the arbitrage opportunity was already gone. We would have to transition from inter- to intra-block arbitrage.

This trading strategy is called backrunning. Instead of awaiting a new block, we listened to the mempool to for transactions considered for inclusion. If we found one that would trigger an arb if confirmed, we would submit the arb transaction directly to the block producer with the exact same gas price as the arb-creator with the goal to be one slot behind in the final block. Because transactions are ordered first by gas price and next by time, this was also a race.

This race was identical to the previous one with one major change on the networking layer. Instead of optimizing for hearing about new containers (blocks) quickly, one needed to optimize for hearing about new additions to the transaction mempool. These transactions were shared with the new AppGossip message type, which were gossiped to both validators and non-validators without weighting by stake. This means that the arbitrageur with the most number of nodes rather than stake could control the mempool.

Fortunately for us, these parameters were released ahead of the Snowman++ launch and we were ready. As the hard fork cut over, we spun up hundreds of full nodes (full nodes do not require any stake and thus are cheap to operate) to virtually guarantee that we were the first to hear about a transaction. Dominant market share was ours once again.

Unfortunately for us, the Ava Labs team realized that treating full nodes and validators with parity perhaps didn’t make much sense. While we weren’t doing anything to impact the performance of the network, if we had wanted to, we easily could have used this configuration to censor transactions and cause other problems without no repercussions.

They quickly shipped an updated version to edit the default AppGossip parameters to sample only validators and ignore full nodes. This meant that it was back to a slightly modified battle for stake where number of nodes rather than absolute quantity of AVAX would anoint the winner.

Alpha decay

Hustle as we could, we eventually saw our market share drop. A few percent here. A few percent there. Soon, we weren’t making enough to pay the massive AWS bills that we were incurring in running a large network of validators and had to resort to running multiple machines on a single Hetzner machine until finally we couldn’t cover that cost either.

A tip of the hat to the smart traders who outcompeted us and are still printing money today. Exactly how you did it continues to nag me to this day. If you ever felt like sharing your side of the story, I could finally lay to rest a little nagging part of my psyche.

Onward

This entire project started with an email inspired by my first blog post. I wish I could be so lucky as to find a second opportunity in my inbox. After a bit of a break, I am beginning to explore this space again. If you are smart and motivated and would like to collaborate, drop me a line. I’ll plan on following this post up with a number of other experiments and side projects that didn’t quite fit into the narrative here, so stay tuned for more. Thanks for reading!